Transform your face with Machine Learning

Last week we explored the possibilities of computer-generated photos of people by using StyleGan2. Today we will have a closer look at how this all works and begin with some fun experimentation. If you haven’t read our previous blog, read it here.
If you want to get straight in the action you can run the colab yourself.
A closer look at the generator
Once the model is trained, the critic part is not important anymore. It is a trained generator that will create magic.
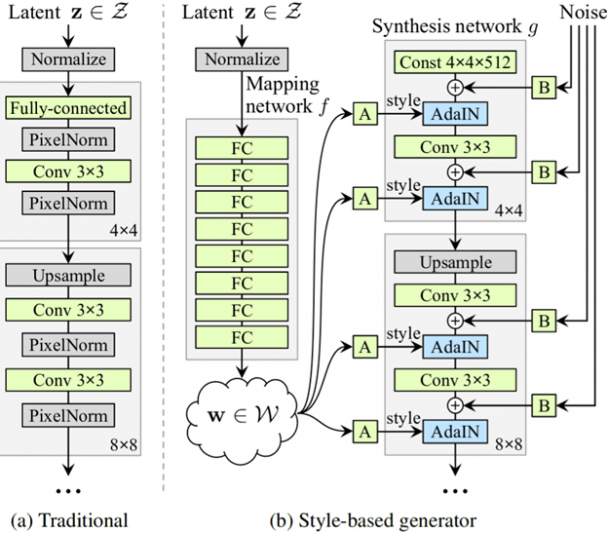
The generator consists mainly of neural layers interconnected with what we call weights. When a model is training it is these weights that are modulated to make it learn. Each layer is like an abstraction. The first layers decide on the fundamentals of the portrait. The direction of the face, and its shape, the further you go through the network the more detailed you go from skin color to freckles and facial hair.

The seed of inspiration (zlatent)
The input of the generator is important. A computer program can’t just randomly come up with totally new faces and variations. It’s all logic and switches and math. So the generator needs an input, a seed of inspiration as you might put it. It consists of a list of 512 random numbers taken out of a normal distribution. So, generate a seed and the network outputs an image. So every possible seed is linked to an image. We call this seed the zlatent.
So by modifying this seed/zlatent we can control what the generator draws.
Example this is the image that is generated at zlatent [0,0,0,0,0,0,0,……..0,0]:

Change on of these zeros to 1 and you get:

It is a totally different person! One might hope by adjusting 1 number in the zlatent we can slowly modify the image (change the smile into a frown for example) but it is really very sensitive and does not seem to be very logically mapped. This is what we call entanglement. Changing the value of one dimension influences a lot of features of the image. This makes it hard to control the generator.
This problem is solved by taking the initial zlatent( the seed of 512 numbers) and mapping it to a 18 X 512 wlatent ( 18 lists of 512 numbers) the model learns this mapping during its training. This wlatent is then fed to the different layers of the generator network giving a more hierarchical control over the generator. This way the features of an image can be mapped to even space giving more control.
By slightly adjusting the wlatent of the second image we can make smaller differences and a relatable images:

So the wlatent gives us a lot more precise control.
To wrap up: every zlatent/seed maps to a wlatent, and that wlatent can then be mapped to an image. By adjusting this wlatent we can control the image.
Push the wlatent a little further:

And stuff starts to become really weird. You can see it as giving the artist too much inspiration!
Projection
Because all this model does is a math function a simple question one might ask is can we get an inverse function. Can we give the model a portrait of a person, turn it upside down and let it search for the right wlatent to create this image? If we can find the wlatent of an actual picture we have levels of control no regular image software program can dream of.
Thankfully stylegan2 has an implementation of this technique called projector.
What we will be using is though is Rolux’s implementation which improves on the original: https://github.com/rolux/stylegan2encoder What it basically does is instead of adjusting the weights of the stylegan generator network( what happens during training) it adjusts the wlatent that then goes through the generator. The loss function is the difference between the generated image and the original portrait.
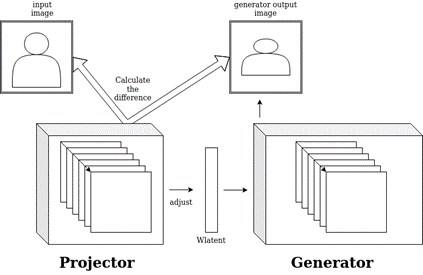
So the projector adjusts the wlatent step by step to come close and closer to the original portrait.
What we end up with is wlatent representation of the original portrait. What is fun about this process is we can take a picture for every step it takes.
Example take our colleague Peter:


It is not pixel perfect but it is so damn close most people will not notice this is not a picture of Peter but a projection of a wlatent. It is such a good visualization of what a machine learning algorithm does.
What is so impressive about this is that stylegan never was trained on any pictures of Peter, but because of the sheer amount of data, stylegan learned it can generate a picture with all of the important features of the original image of Peter: background, facial features, slightly grey hairs….
So lets throw our whole team into the projector:
- https://drive.google.com/file/d/14r6xHjxvVPcjqqSJ4bFPNBP4nMIIzz2G/view?usp=sharing
- https://drive.google.com/file/d/1B_FQv3hfPTpiv-FF6-8F_F3ivmxZ3zHI/view?usp=sharing
- https://drive.google.com/file/d/1gLO0dPTh8XB2aUsPOGYYaayG4Bndvhwg/view?usp=sharing
- https://drive.google.com/file/d/11uNpUM-ME1G3LbAHhMgoL8bBLgUy1RQN/view?usp=sharing
- https://drive.google.com/file/d/1409hK9z7l4h8-H2IpG9LbUYJG-8t1cEU/view?usp=sharing
Now we have a wlatent for everyone in our team. We can start and be a little creative with what we have!
Transformation video
These wlatents exist in what you might call the wspace. And every wlatent represents a point/vector in this space. So what can we do is we can render what it would like to go for a walk along all the points/wlatents and render the journey along the way. What we will get is a cool morphing video that morphs between the faces in a very uncanny way:
Math with faces
What else can we do? Well, we can do some basic math with people’s wlatent. What if we take the average of Joachim and Julie? We do this by simply adding the wlatents and dividing the result by 2:

And now the big question, do I look better if I was 50 % more like Brad?

I will leave that up to you.
The previous examples are smooth blends between all the features of the pictures( head position, hair, background,..)
You can do more advanced calculations by taking the first weight layers from one portrait and the later layers from the other.
For example:
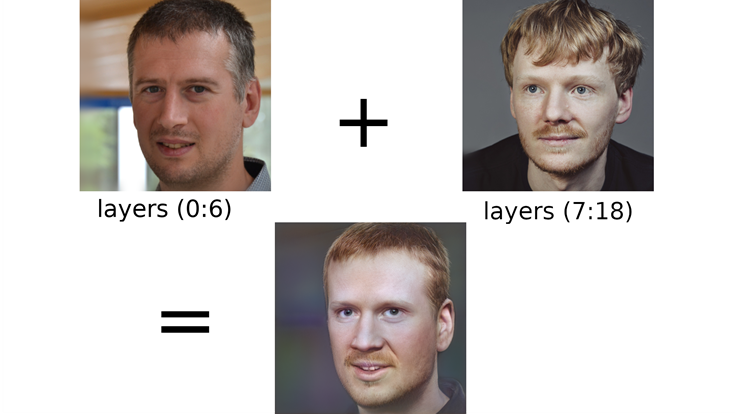
We get head position, hairline, nose, and ears from Peter but skin type and hair color from Greg. Really disturbing! By doing these hard inserts we do get away from the more realistic outputs stylegan2 can generate. You can always experiment with blends of course.
Face deform loops
Another way to walk through this wlatent space is to go for a small walk around a face. I implemented this by adding random offset that to certain layers of the original wlatent and modulating its strength with a simple sin wave function.







